The Two One-Sided t-Test (TOST)
- Details
- Last Updated: Friday, 17 April 2026 15:10
Content
This information leaflet is intended for laboratories performing significance testing for two (mean) values, or for a mean value and a reference value. Unlike the conventional t-test, which assesses whether two values are different, the Two One-Sided Test (TOST) procedure presented here evaluates whether the difference is acceptable - that ism within a specified acceptance range. Deviations in both directions are tested separately using a one-sided t-test at the chosen significance level.
The leaflet has been prepared by the Eurachem Measurement Uncertainty and Traceability Working Group to introduce the use of equivalence testing.
Availability
- Download English version (PDF, 287 kB) (Published 2026-04-17)*
Translation
Translation into other languages is encouraged for members of Eurachem. Other offers of translation should be directed to the Eurachem Secretariat for permission. The Eurachem policy on maintenance and development of Eurachem guidance, available on the Policies page, gives further information on translation.
*Publication dates are dates of website publication. English version first published on this site on 2026-04-17.
Measurement results are only fit for purpose if the reported uncertainty is correct and has a magnitude small enough for the intended use. The target measurement uncertainty (target MU) is the maximum admissible uncertainty defined for a specific measurement goal. This information leaflet provides a short and accessible introduction to the idea of target measurement uncertainty.
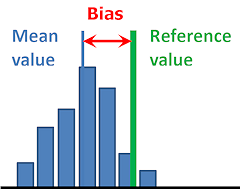Bias is routinely determined during the validation of analytical methods. Usually, the observed bias is not exactly zero. It is then important to decide whether the observed bias can reasonably be treated as unimportant, or whether some further action needs to be taken. This can be particularly difficult to decide when applying the principles of the 'Guide to the Expression of Uncertainty in measurement', which assumes that a correction has been applied for any important bias. 